Homework (Week 7)
Table of Contents
Submission: Due on Friday, 22nd of July, 11am Sydney Time. Please submit using the CSE Give System either online or via this command on a CSE terminal:
give cs3151 hw6 hw6.pdf
Late submissions are accepted up to five days after the deadline, but at a penalty: 5% off your total mark per day.
1 Non-compositional Verification (6 marks)
Here is a three process message passing system presented as a transition diagram of three processes \(P_1\), \(P_2\), and \(P_3\).
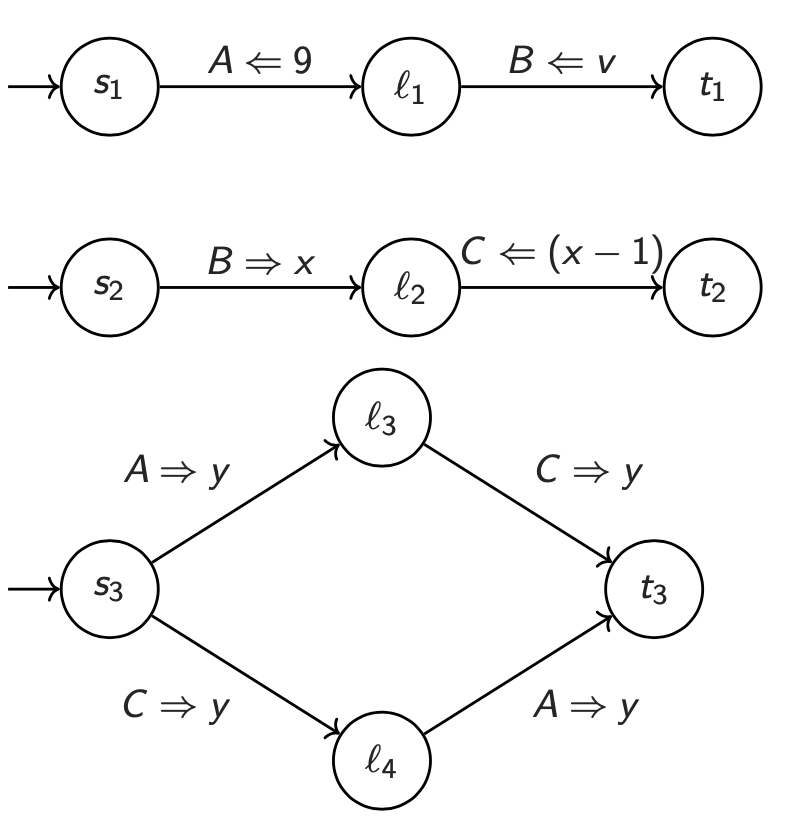
Prove using the Levin and Gries or AFR methods that the following Hoare triple holds:
\[ \{ \textsf{True} \}\ P_1\ \|\ P_2\ \|\ P_3\ \{ y = v - 1 \}\]
You don't need to explicitly discharge your proof obligations; instead, it suffices to give your assertion networks, your extra auxiliary variable wrangling, and (if using AFR) your communication invariant.
2 Termination (6 marks)
Consider the following program:
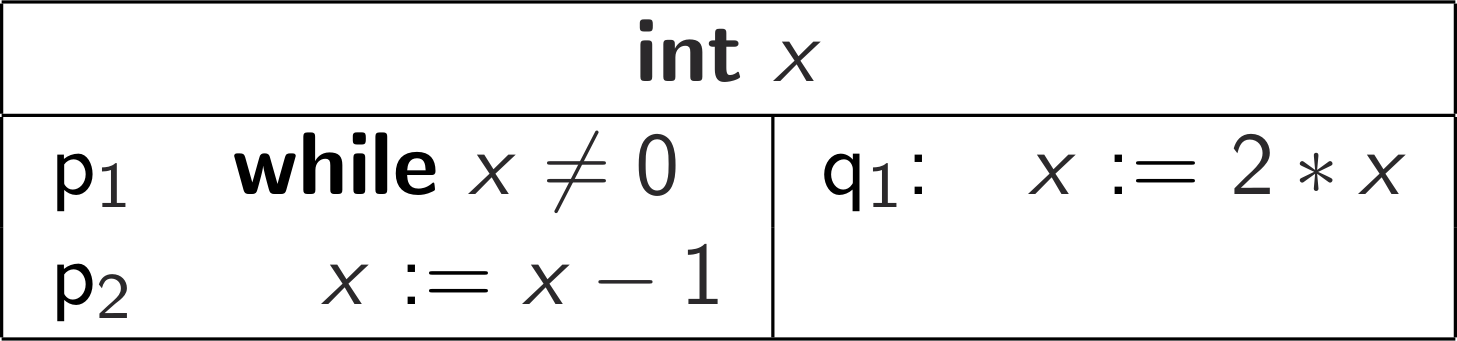
- Use the local method to prove \(x \ge 0\) -convergence for this program. You'll need exit locations for \(p\) and \(q\) (not shown in the above pseudocode). You don't need to explicitly discharge your proof obligations; specifying your assertion networks, your wellfounded set, and your ranking functions is sufficient.
- Is this program \(\top\) -convergent? Briefly motivate your answer.
- Is this program \(\bot\) -convergent? Briefly motivate your answer.
You may assume that the \(x := x - 1\) is executed atomically.
